
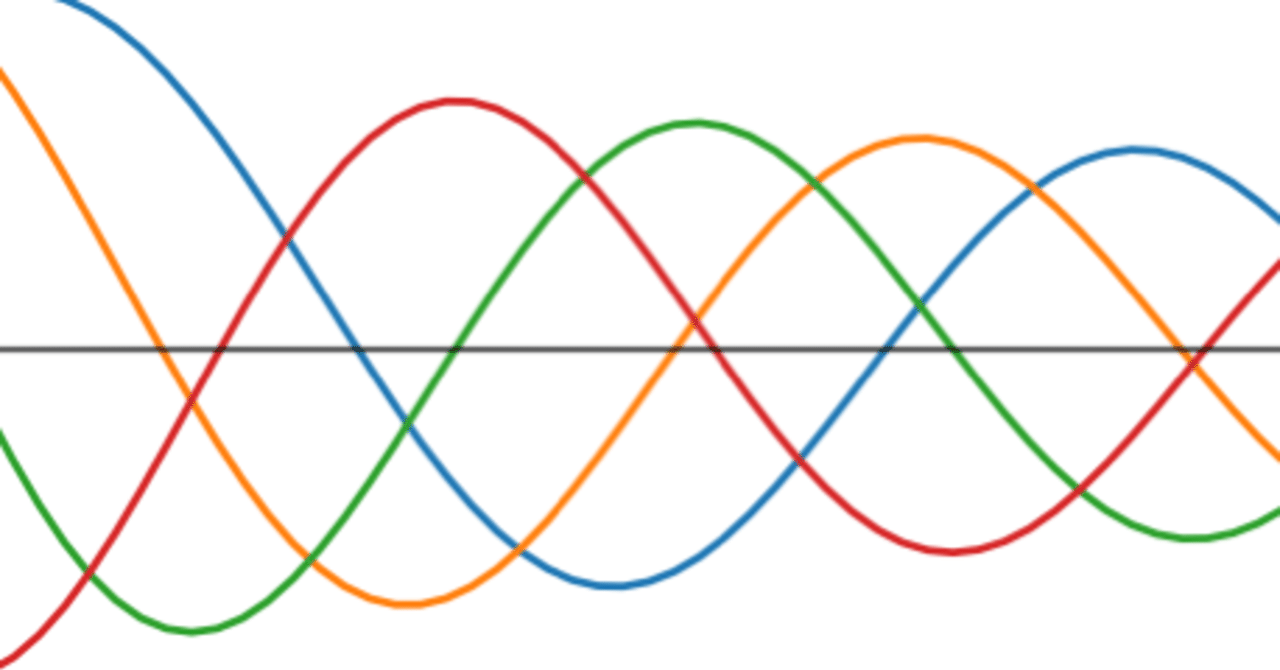
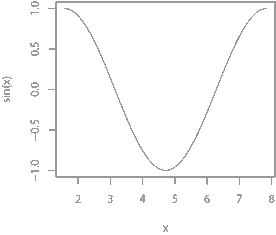
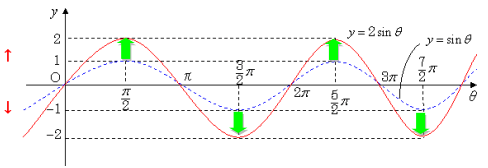
三角関数のグラフの書き方とコツ Sin Cos Tan 周期 理系ラボ
154 関数とグラフ(関数の定義) スキ 2 理一の数学事始め 22年1月10日 1917 フォローしました 今回の説明だけだと初学者にとって分かり 難 にく いと思いますが、前回の説明を踏まえれば理解できると思います。 関数の認識には前回のイメージも大切 よくあるグラフの種類と使い分け 資料や統計の作成に用いられる代表的なグラフと主な使い分け方は以下の通りです。 棒グラフ:データの大きさを比較する 折れ線グラフ:時系列での変化をみる 円グラフ:全体に占める割合をみる 積み上げ棒グラフ
数学 関数 グラフ 種類
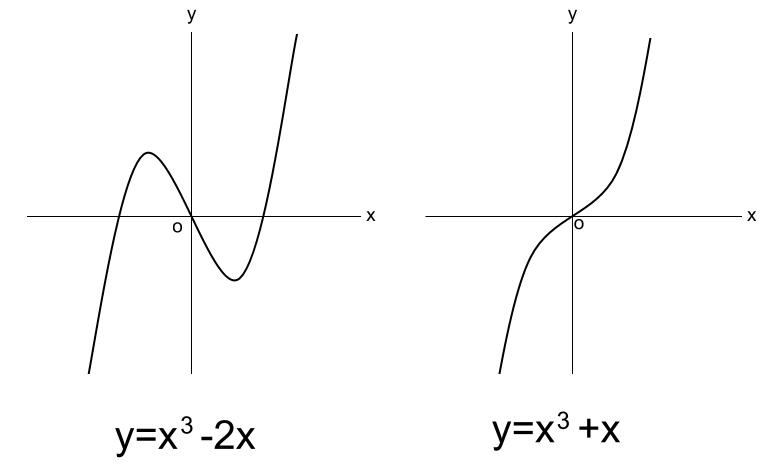
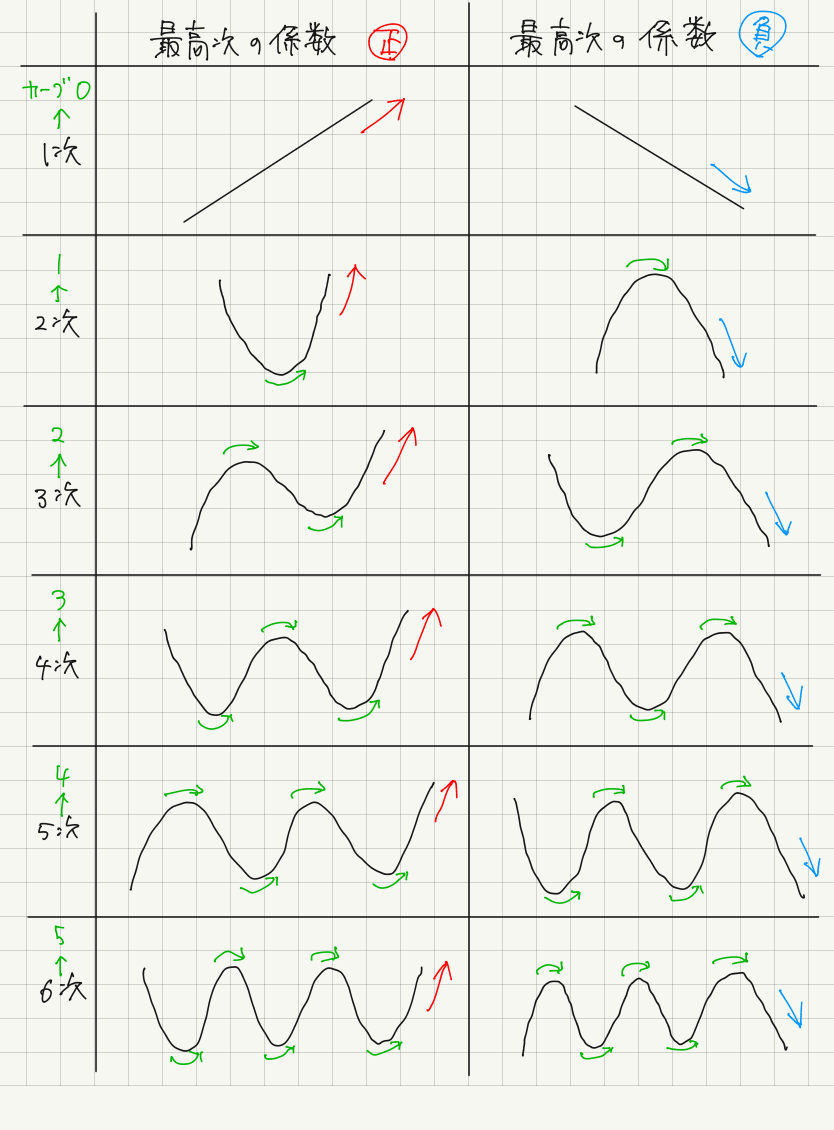
数学 関数 グラフ 種類-言葉だけでは難しいので 「1次関数」と「2次関数」のグラフを見てみましょう。 このように見ると 「1次関数」と「2次関数」 とでは、全く違いますよね。 でも なぜこのようなグラフの差がでるのか! ? それは、出題されている問題によりオイラーの φ 関数 与えられた自然数以下で、その自然数と互いに素な自然数の個数。;
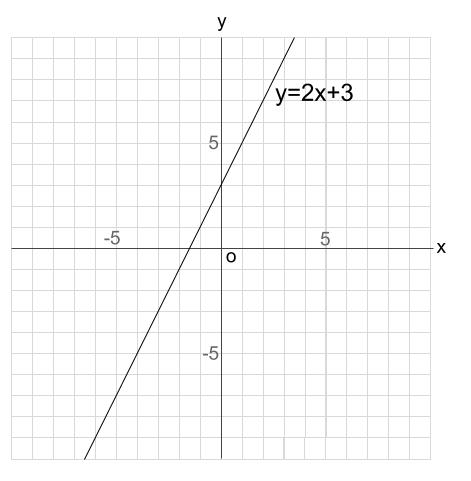
中学数学 1次関数のグラフ 中学数学の無料オンライン学習サイトchu Su
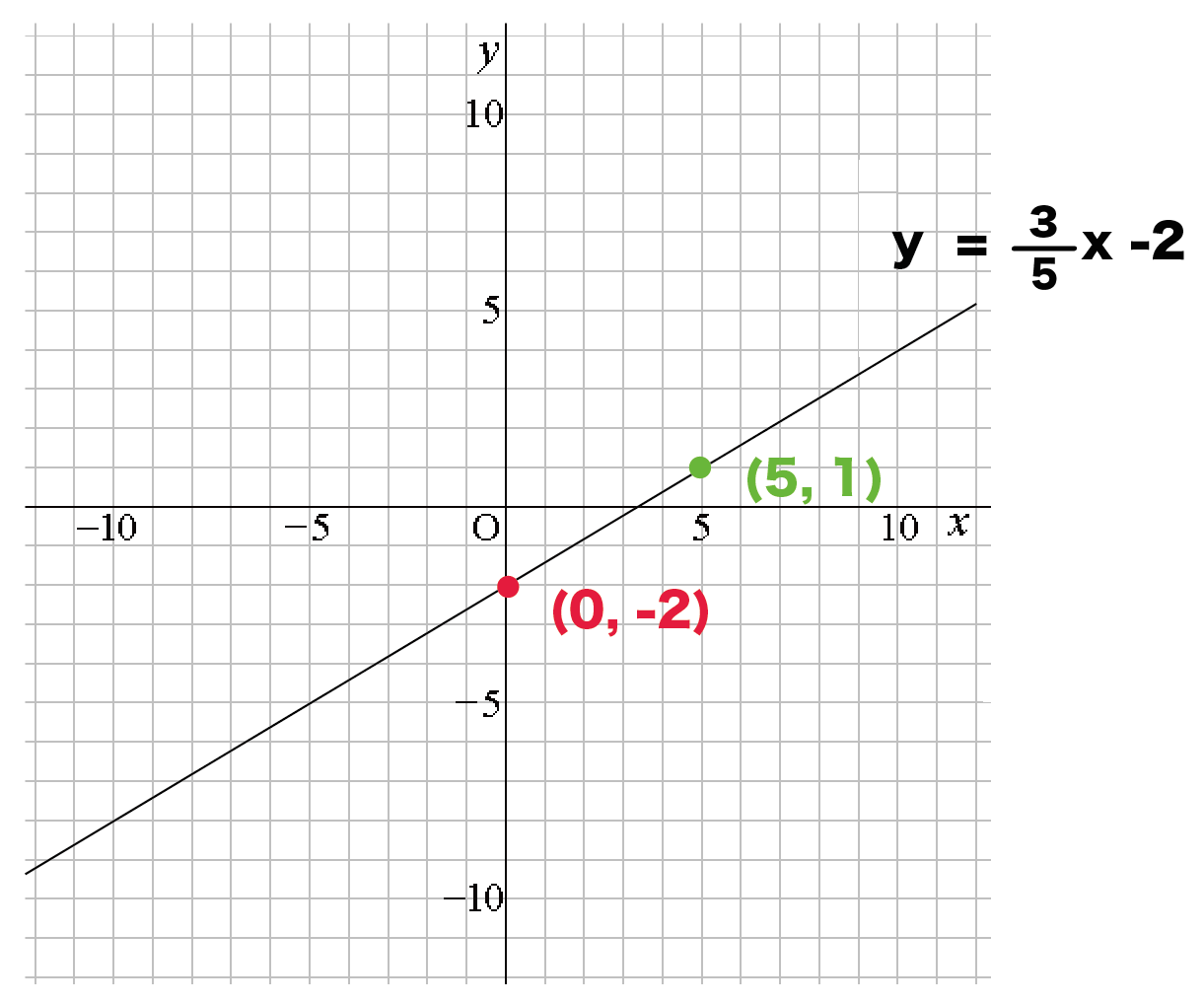
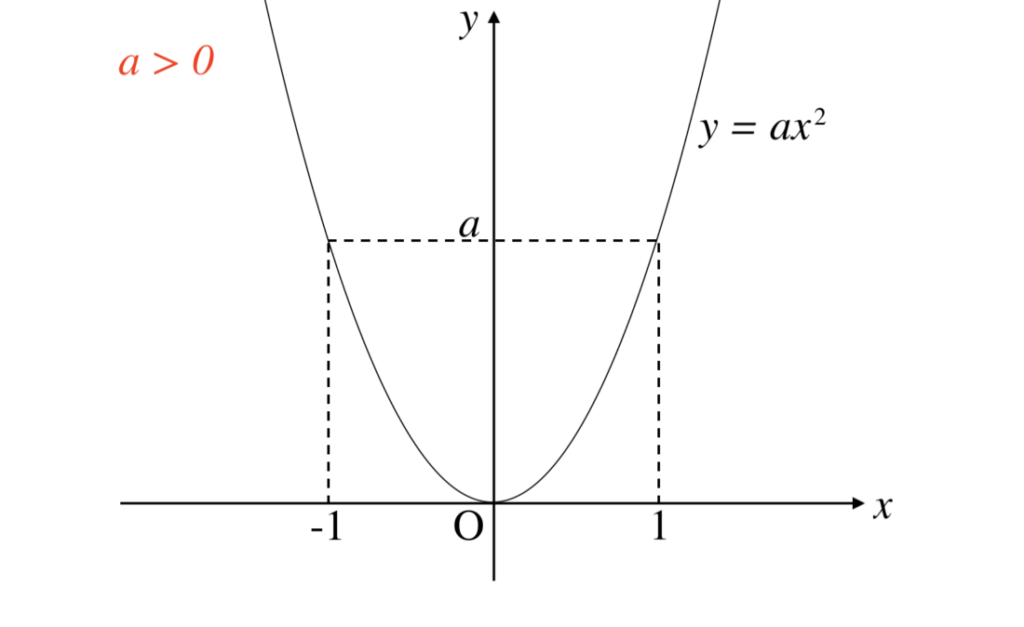
データをグラフで可視化する前に、まずグラフ化の目的を明確化しましょう。 グラフの種類を 目的によって大雑把に分けると、比較、割合、推移、関係性と地理的分布の5つがあります。 目的に合わせたチャート、グラフを選びます。 上図は典型的な 折れ線グラフは、 時間の経過によって数量がどのような変化をしたのか が表されます。 そのため、折れ線グラフの 横軸は時間 を表します。 縦軸は連続量を表すことが多くあります。 算数を究める 1 User 分離量と連続量の意味と違いを知っていますか 一次関数のグラフはとても単純でした。 直線が、斜めに走っているだけです。 そのため、二次関数のグラフは、一次関数のグラフとはまるで別物のように感じる人も少なくありません。 しかしグラフも「 二次関数は一次関数から 1 つ増えただけ 」です。
グラフの種類、次に紹介するのは、「ヒストグラム」と呼ばれるものです。 こちらは、量的データの分布状況を見るのに使われます。 まずデータをいくつかの階級に分け、度数分布表を作った後にグラフ化します。 横軸にはデータの階級が、縦軸には3 13 グラフ 関数の可視化について考える。平面に直行する2 つの座標軸を書き、それぞれx軸と 軸 と呼ぶ。 y x軸上の位置で独立変数の値を与え、また、y軸上の位置で従属変数の値を与え、 (, x y)を座標点とする点の集合を考える。独立変数xが連続的に変域で変化するとき、xにアカデミック 数学 数学の学習:関数とグラフの作成 この種の 数学の問題 では、多項方程式、指数方程式、対数方程式、三角方程式を扱います。 関数の学習では、変化と極限、すなわち、極値と漸近線(あれば)を求め、最終的には方程式をグラフ化
数学 関数 グラフ 種類のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |  合成関数と逆関数の求め方 グラフや特徴を簡単に解説 | 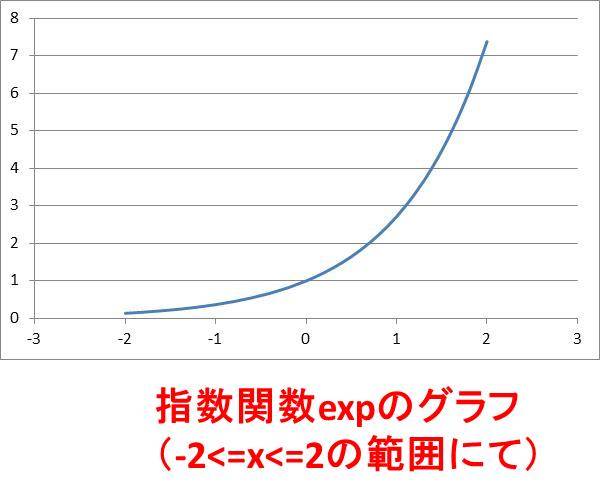 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |
 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |  合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |  合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |
 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |  合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |  合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |
「数学 関数 グラフ 種類」の画像ギャラリー、詳細は各画像をクリックしてください。
 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |  合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |  合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |
 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 | 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |  合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |
 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |  合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |  合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |
「数学 関数 グラフ 種類」の画像ギャラリー、詳細は各画像をクリックしてください。
 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 | 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |  合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |
 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |  合成関数と逆関数の求め方 グラフや特徴を簡単に解説 | 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |
 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 | 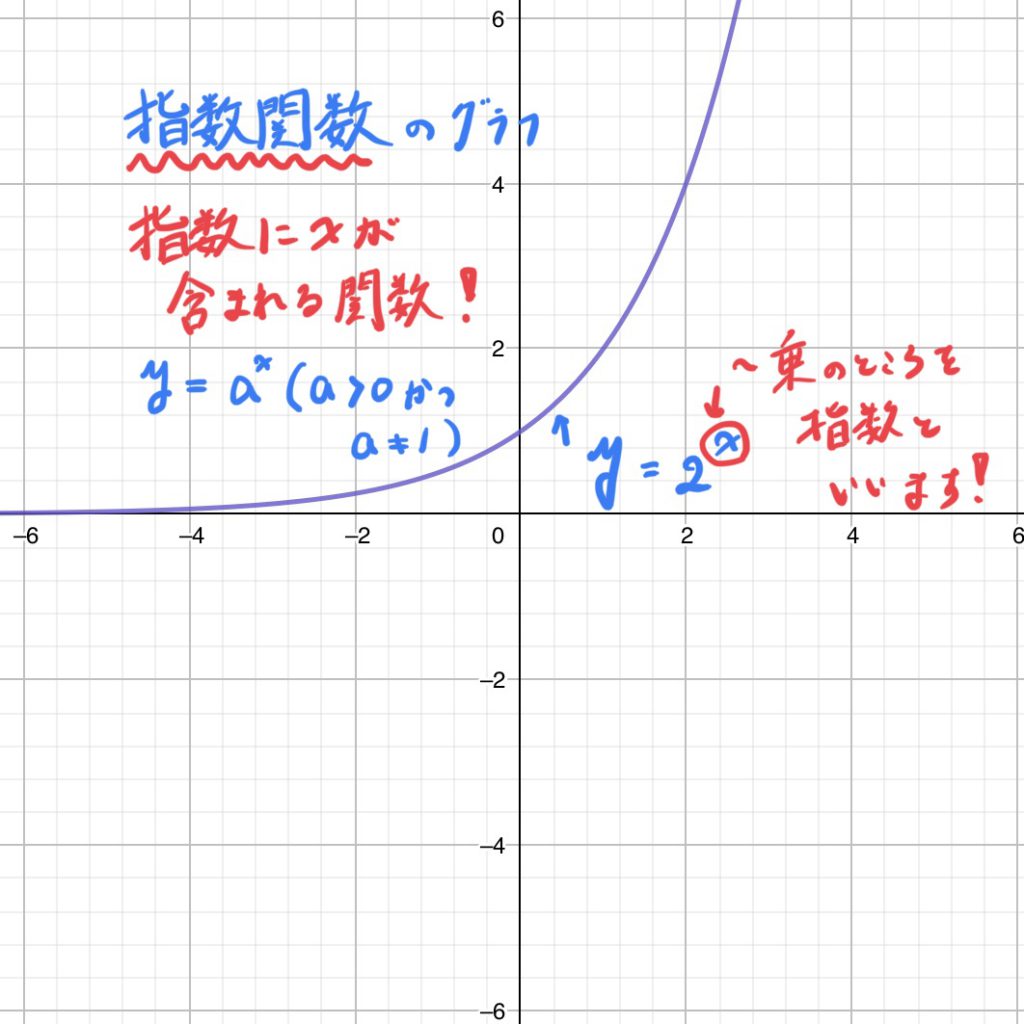 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 | 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |
「数学 関数 グラフ 種類」の画像ギャラリー、詳細は各画像をクリックしてください。
 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 | 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 | 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |
 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |  合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |  合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |
 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |  合成関数と逆関数の求め方 グラフや特徴を簡単に解説 | 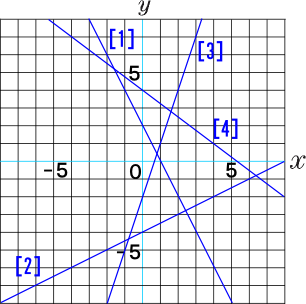 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |
「数学 関数 グラフ 種類」の画像ギャラリー、詳細は各画像をクリックしてください。
 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 | 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |  合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |
 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 | 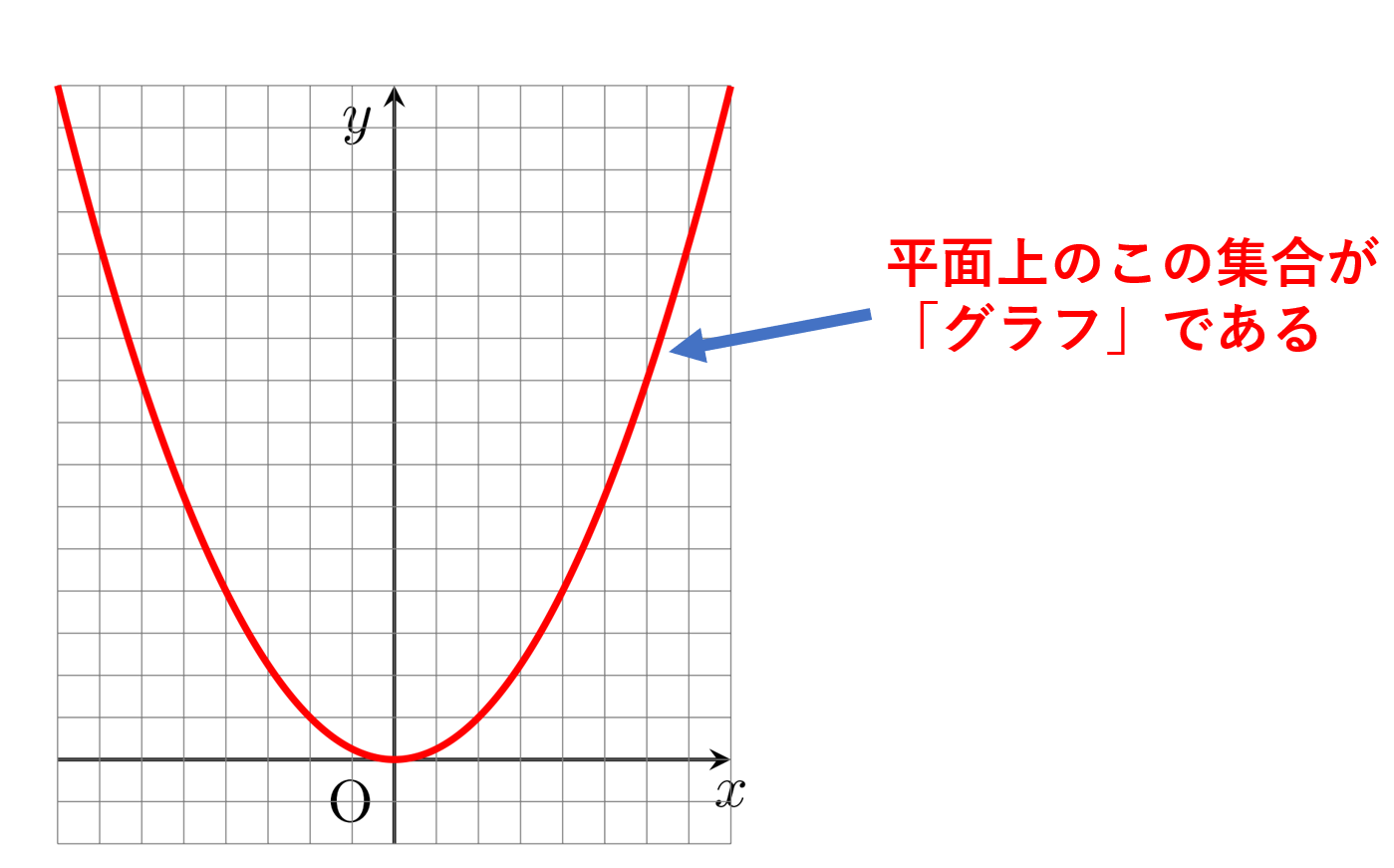 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |  合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |
 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 | 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 | 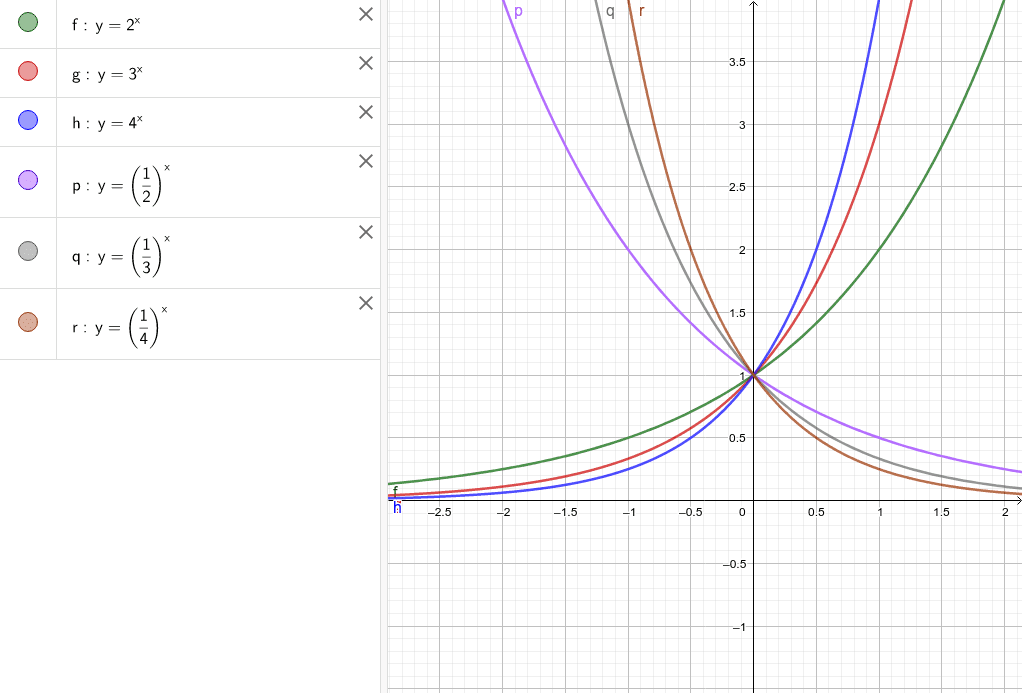 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |
「数学 関数 グラフ 種類」の画像ギャラリー、詳細は各画像をクリックしてください。
 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |  合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |  合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |
 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 | 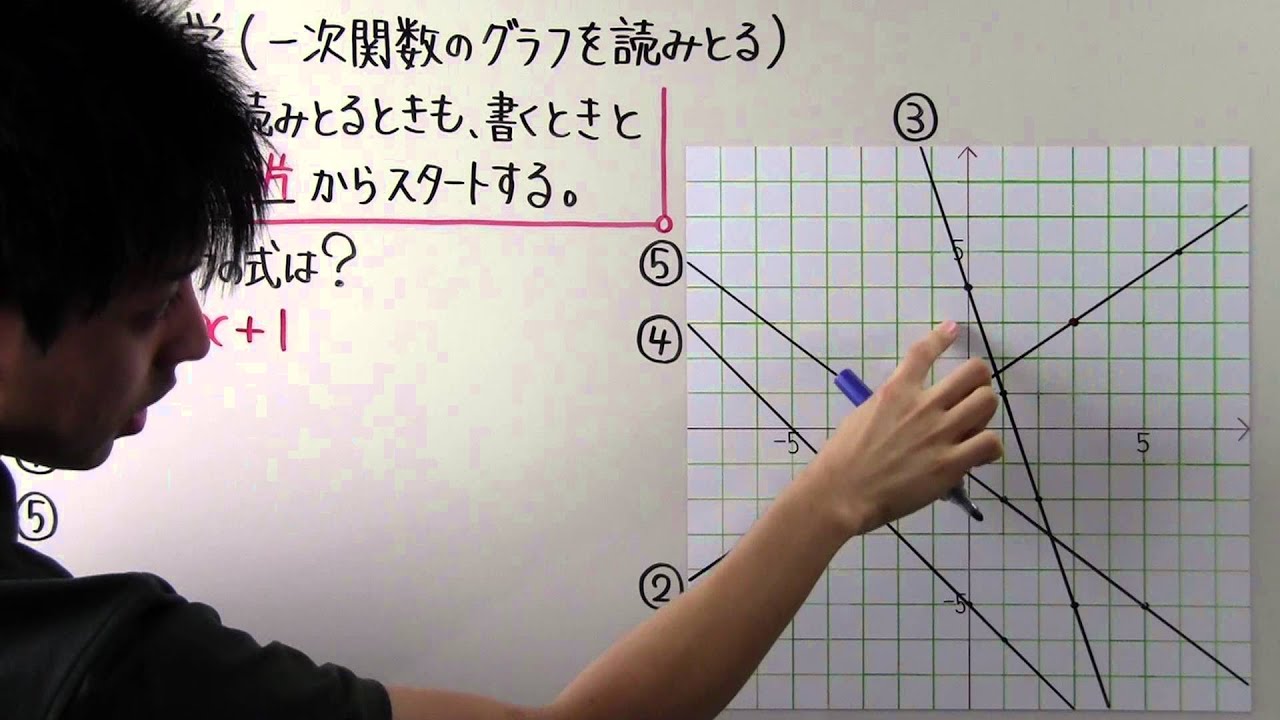 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 | 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |
合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |  合成関数と逆関数の求め方 グラフや特徴を簡単に解説 | 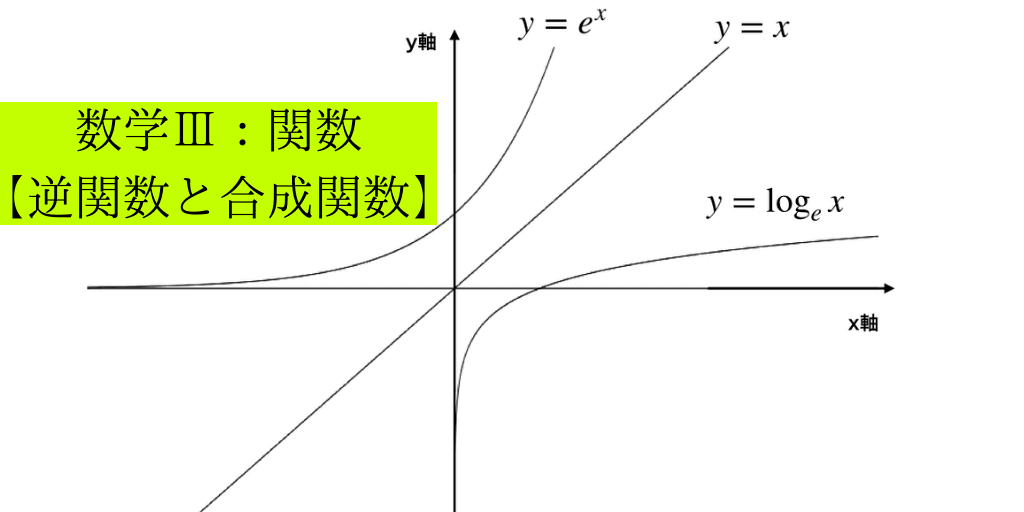 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |
「数学 関数 グラフ 種類」の画像ギャラリー、詳細は各画像をクリックしてください。
 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |  合成関数と逆関数の求め方 グラフや特徴を簡単に解説 | 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |
 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |  合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |  合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |
合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |  合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |  合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |
「数学 関数 グラフ 種類」の画像ギャラリー、詳細は各画像をクリックしてください。
合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |  合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |  合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |
 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |  合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |  合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |
 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |  合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |  合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |
「数学 関数 グラフ 種類」の画像ギャラリー、詳細は各画像をクリックしてください。
 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |  合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |  合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |
 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 | 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 | 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |
 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 | 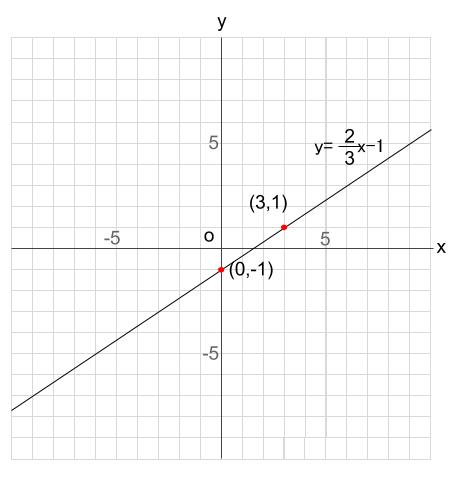 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |  合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |
「数学 関数 グラフ 種類」の画像ギャラリー、詳細は各画像をクリックしてください。
 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |  合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |  合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |
 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |  合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |  合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |
 合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |  合成関数と逆関数の求め方 グラフや特徴を簡単に解説 |
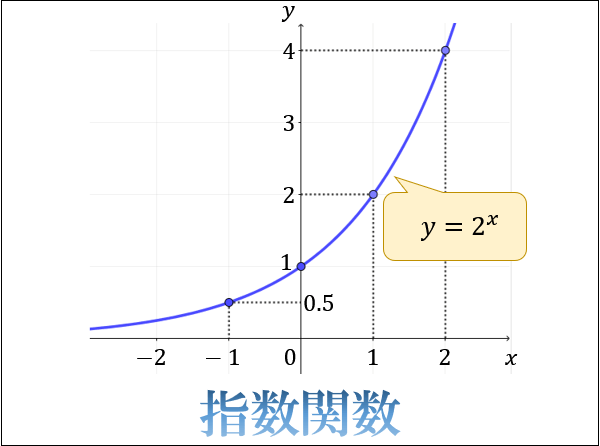
指数関数のグラフを思い浮かべるときには、 の値の変化によって、 の値が急増、緩減すること 0以下にならないこと 必ず1を通ること 底が逆数になると 軸対象になること 底が大きくなると 軸寄りに、小さくなると直線 に近づくこと 対数関数と におい関数の種類 数学関数 Excelにはたいていの数学関数は揃っています。次のような関数はよく使われるので、覚えておいて下さい。普通の使い方と違うのは対数関数でしょ う。普通「log」と書くところ、Excelでは「LN」と書きます。「natural logarighm」の頭文字
Incoming Term: 数学 関数 グラフ 種類,




0 件のコメント:
コメントを投稿